.jpg)
 |  |  |
1.- Coge un trozo cuadrado de papel y dóblalo en cuatro como un acordeón.
|
2.- Dobla el ángulo superior izquierdo hacia abajo.
|
3.- Dobla el extremo derecho de la tira hacia abajo hasta que se junte con el borde doblado anteriormente.
|
 |  |  |
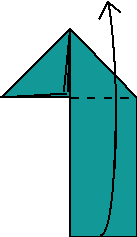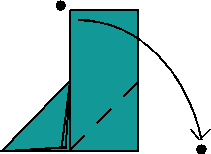4.-Dobla ahora la tira hacia arriba.
|
5.- Dobla la tira ahora hacia abajo y hacia la derecha.
|
6.- Dobla la esquina superior derecha para formar un segundo pico. Ya tienes un módulo terminado.
|
 |  |  |
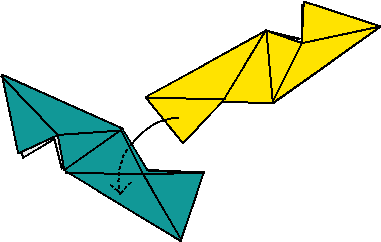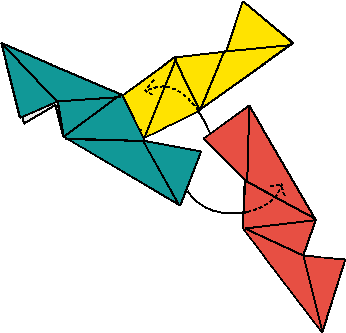7.- Desliza el extremo de un módulo en el costado de otro como se muestra en la figura. La aleta debe de ir entre las capas de papel, los dobleces deben de alinearse.
|
8.-Se necesitan tres módulos para hacer una esquina del poliedro. Desliza un tercer módulo en el segundo, y el primero en el tercero.
|
9.- Esto es lo que debes ver. fíjate como la mitad de cada módulo se usa para hacer esa especie de pirámide.
|
 |  |  |
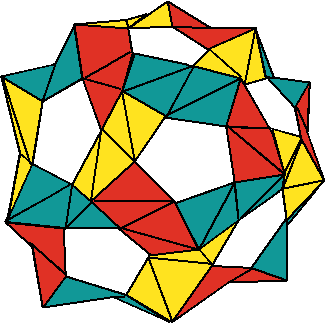10.- Sigue añadiendo módulos fijándote en que cuando tengas cinco módulos alrededor de un hueco debes unirlos para formar un pentágono.
Los picos de las pirámides coinciden con lo que serían los vértices de un dodecaedro.
Se necesitan treinta unidades para conseguir esta figura. Una sugerencia es utilizar papeles DIN A4 del que obtendremos un cuadrado que a su vez dividiremos en 4 partes. De esta forma necesitaremos 8 papeles. Lo tendremos más fácil si utilizamos papeles cuadrados de los usados en los bloques para notas.
Un reto es utilizar tres colores distintos de módulos y conseguir que en cada esquina se entrelacen siempre tres colores diferentes.
| ||
 |  |  |  |
 |  |  |  |
 |  |  |
| Calcular el tamaño de los huecos en relación al grosor del material usado, y al ángulo que giran las caras no es fácil. Para el diseño de las maquetas, he utilizado una aplicación en Java que puedes encontrar en la página de George Hart. En ella puedes encontrar más información sobre este tema y algunas figuras construidas con distintos materiales. |  |
 | Debemos cortar tres de los cuatro triángulos para poder entrecruzarlos. Es conveniente volver a unirlos con cinta adhesiva en cuanto tengamos segura su posición. |  |
 | Esta estructura es un derivado del icosaedro truncado. Para construirla necesitamos 20 triángulos equiláteros en los que realizaremos unos cortes según el modelo. Entrelazaremos las piezas utilizando los cortes correspondientes. |  |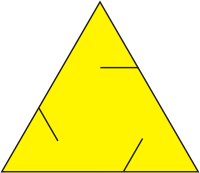
 |
Para construir esta figura necesitamos 30 cuadrados en los que realizaremos unos cortes según el modelo. Entrelazaremos las piezas utilizando los cortes correspondientes (Corte largo se entrecruza con corte corto).
|  |
 |
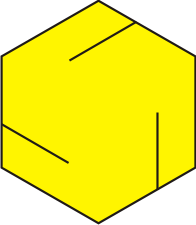
Para esta figura necesitamos 20 hexágonos cortados según el modelo.
|  |
 |
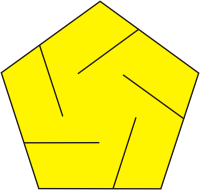
Esta estructura es una especie de dodecaedro. Para construirla necesitamos 12 pentágonos en los que realizaremos unos cortes según el modelo. Entrelazaremos las piezas utilizando los cortes correspondientes.
|  |
 |
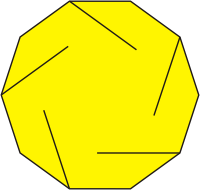
Esta otra figura la conseguiremos con 12 decágonos cortados según el modelo.
|  |
He desarrollado descubrimientos interesantes en la red uno de ellos nos habla sobre algunas de las mujeres compositoras que la historia no h...
