CLASIFICACION Y EVOLUCIÓN ESTRUCTURAS
¿QUE ES UNA ESTRUCTURA? ¿PARA QUE SIRVE? ¿CUALES SON LOS ELEMENTOS DE UNA ESTRUCTURA?
En este breve recorrido daremos respuesta a esta preguntas y a otras mas.
Una
estructura se puede definir como un conjunto de elementos ubicados de
forma que den rigidez y permitan soportar, sin romperse, las cargas o
esfuerzos a las que se ven sometidos.
Las cargas son las fuerzas que se producen en la estructura, imaginate lo que sientes cuando alguien te tira de un brazo, las estructuras se diseñan para soportar cargas, algunas de ellas no cumplen esta condición y colapsan.
CLASIFICACIÓN DE LAS ESTRUCTURAS
Las cargas son las fuerzas que se producen en la estructura, imaginate lo que sientes cuando alguien te tira de un brazo, las estructuras se diseñan para soportar cargas, algunas de ellas no cumplen esta condición y colapsan.
CLASIFICACIÓN DE LAS ESTRUCTURAS
Según su procedencia, podemos encontrar estructuras artificiales y estructuras naturales
Algunos ejemplos de estas estructuras:
Según los elementos que las componen pueden ser:
En la imagen anterior vemos los tres ejemplos de estructuras:
Prácticamente todas las estructuras artificiales son una combinación de al menos dos tipos de estructuras.
- Mesa, silla, puente, grúa, estanterías, edificio, estas son creadas por el hombre.
- Árbol, esqueleto de un animal, hoja, Estas son creadas por la naturaleza.
Según los elementos que las componen pueden ser:
- Masivas, son aquellas que concentran una gran cantidad de material, p.e. la cimentación de un edificio, una pirámide, una montaña.
- Laminares, están formadas por elementos de una gran superficie y poco espesor, p.e. la carrocería de un auto, la carcasa de un celular, una caja de cartón...
- Entramadas, están formadas por elementos de gran longitud en comparación con su grosor. A estos elementos se les denomina perfiles, p.e., un puente, marco de una bicicleta, esqueleto humano.
En la imagen anterior vemos los tres ejemplos de estructuras:
- Los cimientos de un edificio son una estructura masiva, pero los pilares, las vigas y otros elementos de la estructura de la casa son perfiles y las paredes son estructuras laminares; Por lo tanto una casa es una combinación de estructuras masivas, laminares y entramadas.
- Un puente colgante es un ejemplo típico de estructura entramada, aunque los grandes pilares que posee son estructuras masivas, y el tablero o superficie por la que se cruza el puente constituye una estructura laminar.
- Muchas cubiertas de edificios son estructuras laminares, pero para mantener esa estructura en el aire se emplean estructuras entramadas y masivas.
Prácticamente todas las estructuras artificiales son una combinación de al menos dos tipos de estructuras.
Evolución de las estructuras
ACTIVIDAD 1
ANALIZA EL SIGUIENTE TEXTO Y REALIZA UNA PRESENTACIÓN USANDO PREZI, SOBRE LA EVOLUCIÓN DE LAS ESTRUCTURAS.Tambien puedes revisar la siguiente presentación como guia (historia de la arquitectura)
RUBRICA
|
Desempeño superior
|
Desempeño alto
|
Desempeño Básico
|
Desempeño Bajo
|
Presentación PREZI evolución de las estructuras
|
La
presentación entregada muestra los aspectos mencionados en el texto
sobre la evolución de las estructuras, incluye imágenes y se visualiza
correctamente, el estudiante entrega el enlace a tiempo por el vínculo de edmodo
|
La
presentación entregada muestra la mayor parte de los aspectos
mencionados en el texto sobre la evolución de las estructuras, incluye
algunas imágenes y se visualiza correctamente, el estudiante entrega el enlace a tiempo por el vínculo de edmodo
|
La
presentación entregada muestra solo algunos de los aspectos
mencionados en el texto sobre la Evolución de las estructuras, incluye
pocas o ninguna imagen y se visualiza correctamente, el estudiante
entrega el enlace a tiempo por el vínculo de edmodo
Entrega tarde la presentación
|
La presentación entregada es idéntica a la de otro compañero (0% ambos)
No entrega la presentación en el vínculo de edmodo, ni de otra forma (0%)
La presentación muestra pocos aspectos del texto e incluye pocas imágenes poco relacionadas con el texto.
|
 que
pueden soportar una carga con estabilidad. Esto es importante, porque ¿
de qué nos vale hacer un rascacielos si al llegar un golpe de aire , se
nos cae ?
que
pueden soportar una carga con estabilidad. Esto es importante, porque ¿
de qué nos vale hacer un rascacielos si al llegar un golpe de aire , se
nos cae ?Ejemplos de estructuras son, aparte del edificio, una silla, un puente, las torres de electricidad e incluso el caparazón de la tortuga.
Las estructuras tienen que estar diseñadas para soportar las cargas que va a contener, esto es su propio peso mas el peso variable. En el caso del puente, el propio peso es el peso de los elementos que lo componen y el variable son los vehículos que circulan por el mismo.
Hay veces que aparecen fuerzas repentinas como vientos o movimientos de tierra. Un buen arquitecto tiene que tener en cuenta estos factores a la hora de su diseño.
Tipos de esfuerzos
Las fuerzas que pueden aparecer en una estructura pueden ser:
Tracción. Ocurre cuando aparecen fuerzas que tienen a alargar a un elemento de la

estructura. Un ejemplo claro es el cable
que soporta el peso de un puente. Por un lado está la viga que soporta
la carretera y por el otro el pilar al que está amarrado
Compresión. En este caso, la fuerza tiene a disminuir la longitud del elemento. Ejemplo, la pata de una silla


Torsión.
En este caso, la fuerza que aparece es circular y tiende a retorcer el
material. Un ejemplo lo tenemos en la llave de una cerradura o un
destornillador Cizalla. Las fuerzas son paralelas, de sentido contrario y perpendiculares al elemento
Cizalla. Las fuerzas son paralelas, de sentido contrario y perpendiculares al elemento
Ejercicio. Nombrar 2 ejemplos donde aparecen cada uno de los esfuerzos estudiados. Ejemplo, tracción en la cadena del ancla de un barco. Cizalla. Las fuerzas son paralelas, de sentido contrario y perpendiculares al elemento
Cizalla. Las fuerzas son paralelas, de sentido contrario y perpendiculares al elemento
Elementos de una estructura
Desde un puente a un rascacielos encontramos que toda estructura tiene una serie de elementos que casi siempre se repiten en todos ellos. Pasaremos a comentarlos- Cimientos. Donde recae todo el peso. Suelen estar formados por un entramado de hierros y hormigón y sirve de base para soportar todo el peso de la estructura. La forma y el tamaño dependen de qué va a soportar. No es lo mismo para un puente sobre el mar que para una casa.
 Columnas.
Elementos verticales que partiendo de los cimientos elevan la
estructura. En un edificio, las de abajo son mas anchas que las de
arriba, debido a que a medida que subimos plantas, el peso que soporta
es menor
Columnas.
Elementos verticales que partiendo de los cimientos elevan la
estructura. En un edificio, las de abajo son mas anchas que las de
arriba, debido a que a medida que subimos plantas, el peso que soporta
es menor- Vigas. Parecida a las columnas, pero en este caso se colocan horizontalmente. Las vigas que hay entre dos vigas se llama vigueta
 Arcos. Elemento
muy usado en la antigüedad, permite soportar un peso de la estructura
“descargándolo” sobre los extremos. Vemos un ejemplo de nuestro puente
de Alcantara
Arcos. Elemento
muy usado en la antigüedad, permite soportar un peso de la estructura
“descargándolo” sobre los extremos. Vemos un ejemplo de nuestro puente
de Alcantara- Tirantes. Son cables de acero especial que soportan un gran esfuerzo de tracción. Se suele emplear mucho en los puentes
Arcos.Como vimos antes, el arco se emplea para soportar un elemento horizontal “descargando” este peso sobre los dos pilares laterales. Hasta aquí todo bien, el misterio está en que cada piedra que compone el arco está suelta. Entonces, ¿ porqué no se cae ?.
La respuesta está en la forma de las piedras, que no son bloques rectangulares, sino que tiene los lados de diferente tamaño y de esta forma al posicionarse sobre el arco, el lado mayor se coloca en la parte superior y el menor en la parte de abajo del arco.
A la piedra superior se le llama piedra clave. Veremos en la siguiente ilustración este detalle.
 La
“clave ” de esta piedra clave radica en cómo transmite la fuerza
vertical a otras horizontales. Lo podemos ver en este detalle
La
“clave ” de esta piedra clave radica en cómo transmite la fuerza
vertical a otras horizontales. Lo podemos ver en este detalleEstructuras Estables e Inestables.
Decimos que una estructura es estable cuando ante cualquier esfuerzo repentino ( empuje ) recobra su posición original.Cristina Sierra Moreno ( 1º Bachillerato 2012 ) nos ha hecho un trabajo con el GIMP para mostrar este concepto. Podemos verlo a continuación.

En el muñeco de la izquierda vemos que al empujarlo no se cae. Es muy estable y su estabilidad se debe a dos cosas
- La base permite recuperar su estado inicial
- El centro de gravedad lo tiene muy bajo
 El
centro de gravedad es un punto virtual ( imaginario ) donde se supone
que esta toda la masa del cuerpo. Esto es, desde el punto de vista de la
gravedad, es como si tirase de ese punto.
El
centro de gravedad es un punto virtual ( imaginario ) donde se supone
que esta toda la masa del cuerpo. Esto es, desde el punto de vista de la
gravedad, es como si tirase de ese punto.Si un coche que tiene motor se cae al agua, el punto de entrada es por el capó, ya que la mayor parte del peso esta en la parte delantera ( motor ).
Si encontramos el centro de gravedad y lo “sujetamos” con un boli, entonces, el objeto no se cae ( ver imagen )
Perfiles
Algunos de los elementos de las estructuras como las vigas tienen formas muy características. A esta forma se le denomina Perfil.Podemos hacer este perfil como un cuadrado macizo de hierro para que soporte el peso, pero, ¿ No habrá otra manera de usar menos material y que soporte el mismo peso ?.
Los ingenieros mecánicos ya se plantearon este asunto y descubrieron que la Forma del perfil es determinante, o sea que a esa barra maciza le quitamos el hierro del interior y tenemos una barra cuadrada hueca con resultados fabulosos.
Mostramos algunos de los perfiles mas usados en la construcción

La primera de ellas es la cuadrada hueca, la segunda la doble T ( también llamada H) , la tercera la T y la cuarta la L. Hay muchas otras, pero quizás estas son las mas usadas de todas.
Fuerzas.
Para terminar este tema vamos a estudiar un poco cómo actúan las
fuerzas en los elementos mas sencillos, como una viga, para determinar
como se reparte el esfuerzo en el mismo. Ponemos un ejemplo.Si tenemos soportar un peso en el centro de un puente de 1000 Kg, y el puente está apoyado por dos pilares, ¿ Qué esfuerzo soporta cada pilar ?.
Respuesta: Como el peso dista lo mismo de cada pilar y como hay dos, el esfuerzo en cada uno es 500 kg.
Veremos otras situaciones un ” pelín ” mas complicadas.
Ejercicio. Calcular
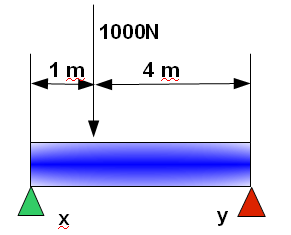 que esfuerzo soporta el apoyo X y el apoyo Y si la fuerza de 1000 Nw está a 1 metros de X.
que esfuerzo soporta el apoyo X y el apoyo Y si la fuerza de 1000 Nw está a 1 metros de X.Solución:
a) Se cumple que las fuerzas hacia arriba son iguales que las fuerzas hacia abajo y por tanto, 1000 = Fx + Fy
b) Si quitamos el punto de apoyo X, entonces la barra se caería por la izquierda. Tenemos que sujetarla para que no se caiga. Si la sujetamos justo debajo de la fuerza de 1000 Nw, la fuerza necesaria para evitar que se caiga sería también de 1000 Nw. Si nos alejamos del punto a la izquierda vemos que la fuerza que tenemos que emplear decrece. Esto es , a mas lejos, menos fuerza para evitar que se caiga. Por tanto, y aplicando la ley de la palanca, tenemos que:
Pero como nos hemos desplazado 1 metro a la izquierda, el punto Y también va a trabajar, y por tanto tenemos que hacer de nuevo los cálculos para este punto. Bueno, como dijimos al principio que la suma de las fuerzas es 1000 tenemos que Fy va a ser 200 Nw, pero sería bueno que hagáis los cálculos para comprobarlo.
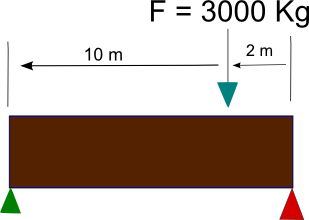 Ejercicio 2.Calcular como se reparten el peso los puntos verde y rojo de la imagen. Ejercicio 2.Calcular como se reparten el peso los puntos verde y rojo de la imagen. |
|||||
 Ejercicio 3. Calcular el peso que recae sobre los apoyos si las fuerzas que actúan sobre la barra son 100 y 200 Kg. Ejercicio 3. Calcular el peso que recae sobre los apoyos si las fuerzas que actúan sobre la barra son 100 y 200 Kg. |
|||||
 Ejercicio
4. Hemos fabricado dos soportes con dos tipos de plástico diferente.
Uno de los soportes aguanta un peso de 200 Kg y el otro de 100 Kg. La
longitud de la barra es 10 metros. Resolver los siguientes supuestos.a)
Calcular la distancia al soporte del izquierdo si el la fuerza es 400
kg) Calcular la fuerza máxima que puede soportar en el caso de que la
distancia sea 2 metros. Ejercicio
4. Hemos fabricado dos soportes con dos tipos de plástico diferente.
Uno de los soportes aguanta un peso de 200 Kg y el otro de 100 Kg. La
longitud de la barra es 10 metros. Resolver los siguientes supuestos.a)
Calcular la distancia al soporte del izquierdo si el la fuerza es 400
kg) Calcular la fuerza máxima que puede soportar en el caso de que la
distancia sea 2 metros. |
|||||
 Haciendo estructuras mejores. Viva el Triángulo ¿ Como hacer resistentes a las estructuras ?
Haciendo estructuras mejores. Viva el Triángulo ¿ Como hacer resistentes a las estructuras ?Bueno, mejor sería hacerse la pregunta ¿ Cómo hacer estructuras resistentes al menor precio ?.
Todos podemos hacer un edificio resistente incorporando unas columnas enormes con unos cimientos muy profundos, pero el precio sería muy alto. La idea es hacer la estructura para que con el menor material posible, soporte el peso para el que han sido diseñados. Aquí interviene de forma determinante, la forma de la estructura. Veremos una de ellas, el triángulo.
Si hacemos un cuadrado con barras de metal y las unimos unas a otras con tornillos, podemos hacer el experimento de aplicar fuerzas en los vértices. Resultado-> Los lados ceden.
Si hacemos lo mismo con un triángulo ( usamos menos barras y menos material ) el resultado es bien distinto. Tenemos una forma geométrica que soporta muy bien los esfuerzos que tienen a deformarlo.

En esta imagen se muestra un detalle del puente colgante de portugalete ( Vizcaya ) donde aparte de varios tirantes, podemos observar que la estructura está muy triangularizada, o sea, existen muchas formas triangulares en el mismo. Podemos hacer la misma observación en la torre Eiffel, edificios y otras estructuras y veremos lo mismo. Triángulos. ¿ Porqué no cuadrados ?.Veremos la razón. Lo veremos mejor en este ejemplo.

En los dos ejemplos hemos aplicado una
fuerza , primero a un cuadrado y luego a un pentágono. Tenemos el mismo
resultado, una deformación de la forma original. Si pasamos a
triangulizar y ponemos el elemento verde, el resultado son dos
triángulos donde había un cuadrado y lo mismo del 2º ejemplo ( en este
caso 3 triángulos). Si aplicamos de nuevo la fuerza externa, la nueva
estructura soportará el esfuerzo mucho mejor.
Ejercicios. En los siguientes elementos, comenta si es estable y como se puede hacer

Merece la pena, para terminar esta sección,
ver este vídeo donde se muestra el proceso constructivo de un puente
sobre el Tajo para el AVE. Una maravilla.
http://vimeo.com/67119686















![final[1].jpg final[1].jpg](https://geogebramad.wikispaces.com/file/view/final%5B1%5D.jpg/223703878/365x572/final%5B1%5D.jpg)

















Las correcciónes van en fuxia. La definición de módulo y redes estan bien, el arte musulmán también, pero teneis que revisar el enfoque del tema de la aplicación del módulo al diseño, arquitectura y embaldosados, y las imágenes de Escher que sean en relación al módulo, justo las que no habeis seleccionado.
Última corrección: Esta bastante completo el trabajo, pero os ha faltado jerarquizar los títulos con un subrayado y negrita común en todo el trabajo así como el mismo tipo de letra.
Voy a haceros correcciones individuales para que veais en qué podeis mejorar. Las partes que esten mal o no se correspondan con el tema las pondré en rojo y las que son demasiado extensas y con lenguaje demasiado complejo en verde para que las resumais cara al powerpoint.
1. Definición de módulo: Un modulo es objeto un elemento visual autosuficiente, con carácter propio que puederepetirse para formar una composicion mayor.
La palabra "modulo" es usada con diferentes acepciones.
Un módulo es por lo tanto la mínima forma funcional o visual que es posible indentificar.
La definición esta bien, solo falta un poco de orden en la estructura del texto, título (subrayado y en negrita y punto y a parte).
Falta la definición de submódulo
2. Redes modulares básicas.
Los módulos han sido elementos que se han empleado a lo largo de la historia del arte y el diseño para crear composiciones estructuradas y ordenadas. Los módulo puede ser: formas geométricas (polígonos, estrellas, circunferencias, etc) o formas orgánicas. Las estructuras modulares pueden ser de dos clases: simples y complejas. Las estructuras modulares simples están formada por la repetición de una sola figura: triángulo, cuadrado, etc.
Las cuadriculas de un diseño de repetición se llaman redes modulares o mallas. Pueden tener diferentes formas y combinaciones , pero las fundamentales son las formadas por cuadrados o triángulos equiláteros. Los módulos pueden ser orgánicos o geométricos. Los módulos se originan a partir de polígonos regulares que se pueden repetir, combinar o enlazar.
3. Redes modulares complejas.
Las estructuras complejas están formada por la yuxtaposición de varias figuras geométricas o por la superposición de varias figuras.
Generalmente se usan polígonos regulares y en la mayoría de las ocasiones se generan por la combinación de redes simples.
Su uso se centra en el diseño, numerosos elementos de los que nos rodean siguen estructuras modulares, ejemplo son los ladrillos de las construcciones, los azulejos, diseño de joyas, etc.
¡¡¡Faltan Imágenes!!! La teoría esta bien hecha pero tenías que haber diferenciado los títulos jerarquizando así el texto.
4. El módulo y la ornamentación. Ejemplos en el arte musulmán. En la pavimentación....
EL ARTE MUSULMÁN.
Debido a que la religión musulmana prohíbe terminantemente la representación de seres vivos (humanos, vegetales o animales) los artistas musulmanes no tuvieron otra opción que enfocarse en el desarrollo de formas geométricas, en este caso, los famosos mosaicos.
Utilizan una decoración exuberante, utilizan mucho los elementos vegetales estilizados. Trabajan el yeso, que es mucho más fácil que el mármol, dándole la misma apariencia.
Sin embargo, los mosaicos son mucho más que sencillos rompecabezas gigantes; son el paradigma de una ciencia medieval extremadamente avanzada y sofisticada.
La simetría casi perfecta de los mosaicos demuestra que los artesanos musulmanes dominaban la regla y el compás, herramientas indispensables para poder crear los intricados patrones llamados “girihs”. Estos girihs están compuestos por cinco polígonos continuos: un decágono, un pentágono, un hexágono, un diamante y una figura “corbata”. A pesar de su complejidad, era relativamente fácil reproducir los diseños a menor escala, lo intrigante es el proceso de escala que utilizaban los artesanos musulmanes para proyectarlos a gran escala sin distorsionarlos exageradamente. Los mosaicos árabes son una perfecta fusión entre el arte y la matemática.
Muchas de las paredes de los edificios islámicos medievales tienen decoraciones geométricas con estrellas y polígonos, a los que a menudo se superponía una red de líneas en zigzag.
Estos son unos ejemplos del arte musulmán.
El arte musulmán emplea redes modulares en las composiciones de sus zócalos de azulejos, con un dominio espectacular de la geometría.
Este es un ejemplo de un mosaico de la división de una circunferencia en ocho partes iguales y del octógono formado al unir los puntos divisorios.
Estos son unos ejemplos de la división de la circunferencia en seis partes iguales y del hexágono formado al unir los puntos divisorios.
Esta bastante bien resumido y relacionado con el tema que nos ocupa que es el módulo. Bien hecho.
El modulo se puede emplear para muchas cosas entre ellas la arquitectura y la industria.Modulo en la arquitectura
MODULO VITRUVIANO
Se llama modulo a la unidad de medida que relaciona la diversas partes de una construcción arquitectónica. En la arquitectura clásica el módulo es el radio del fuste de las columnas fundamentales tomado en la parte inferior o cerca de la basa. Así cuando se dice que una columna tiene catorce módulos se quiere expresar que su altura es catorce veces mayor que el radio. En la arquitectura ojival el módulo era más complicado: consistía en un octógono y antes, en la arquitectura románica, en un hexágono dentro del cual se inscribían un triángulo y otras figuras geométricas. De sus lados se derivaban todas las medidas proporcionales de los miembros del edificio por medio de un procedimiento complejo.
Modulo en la industria
Ejemplo:
VIDRIO
¿Qué tiene que ver esto con el módulo del que estamos hablando? ¿Te has leido el trabajo de tus compañeros? La parte del módulo en arquitectura se ajusta un poco a lo que estamos tratando pero esta del vidrio no se ajusta nada. Tenías que haberle dedicado más tiempo a la búsqueda y hubieras encontrado muchas cosas interesantes. Te falta además adjuntar imágenes ilustrativas.
Un pedazo de vidrio natural encontrado en una playa de Escocia
El vidrio es un material duro, frágil, transparente y amorfo que se usa para hacer ventanas, lentes, botellas y una gran variedad de productos.
El vidrio se obtiene por fusión a unos 1.500 °C de arena de sílice , carbonato de sodio y caliza.
El término "cristal" es utilizado muy frecuentemente como sinónimo de vidrio, aunque es incorrecto debido a que el vidrio es un sólido amorfo y no un cristal propiamente dicho. Es un material inorgánico y tiene varios tipos de vidrio.
MAURITS CORNELIS ESCHER Bien realizado, completo, hubiera estado perfecto si en las fotos hubieses incorporado una leyenda explicando cada imagen.
Es uno de los más grandes artistas gráficos. Nació el 17 de Junio de 1898 en Leeuwarden (Países Bajos) y murió con 73 años el 27 de Marzo de 1972 en Baarn (Holanda).
Era hijo de un ingeniero hidraúlico. Escher destacaba en las clases de dibujo. En 1919 empezó a estudiar arquitectura en Haarlem, pero abandonó sus estudios para ser profesor de Artes Graficas.
Es conocido por sus grabados en madera, xilografías y litografías que tratan sobre figuras imposibles, teselaciones y mundos imaginarios.
A lo largo de su carrera realizó más de 400 litografías y grabados en madera, y también unos 2.000 dibujos y borradores.
La mayor parte de sus obras se caracterizan por la dualidad y la búsqueda del equilibrio, la utilización del blanco y el negro, la simetría, el infinito frente a lo limitado, el que todo objeto representado tenga su contrapartida.
Escher viajó por diversos países de Europa, sobre todo por Italia donde acabó estableciéndose durante 10 años en la ciudad de Roma (1924-1934). Además de Italia conoció el Sur de Francia y España. Precisamente en nuestro país encontró una de sus mayores fuentes de inspiración: la Alhambra. Los precisos e intrincados detalles ornamentales fueron la viva imagen de los esquemas geométricos que tanto le entusiasmaban. Se puede decir que a raíz de su visita a la Alhambra y a la mezquita de Córdoba la obra de Escher, que se había basado en la representación de paisajes hasta entonces, varió su rumbo hacia los dibujos matemáticos que tan famoso lo han hecho. Tras su larga estancia en la capital transalpina se trasladó a Suiza, luego a Bruselas (1937-1941) y más tarde a Baarn, donde residiría hasta su muerte.
Su trabajo fue cobrando reconocimiento, sobre todo, durante los últimos años de su vida y actualmente ha adquirido tal fama que incluso se venden posters, puzzles, camisetas y corbatas con sus dibujos como tema.
Sus obras de arte:
OBRAS RELACIONADAS CON EL MÓDULO: