Estímulos Musicales....: estructuras modulares

martes, 10 de febrero de 2015

ESTRUCTURAS MODULARES TRIDIMENSIONALES- POLIEDROS

POLIEDROS
	Estructura dodecaédrica con módulos PhiZZ: Construcción con módulos realizados en papiroflexia, no necesita pegamento. Construcción paso a paso.
	Estructuras poliédricas 1: elaboradas con piezas de cartulina entrelazadas. No se necesita pegamento. Plantillas listas para imprimir.
	Estructuras poliédricas 2: elaboradas con piezas de cartulina entrelazadas. Necesitaremos cinta adhesiva. Plantillas listas para imprimir.
	Estelaciones del Icosaedro: Diagramas para realizar maquetas en papel de Poliedros Estrellados derivados del Icosaedro.	Galería
	Estelaciones del Dodecaedro: Diagramas para realizar maquetas en papel de Poliedros Estrellados derivados del Dodecaedro.	Galería
	Instrucciones para realizar una maqueta de las lámparas de diseño danés I.Q.Light* que se venden desmontadas y con cuyas piezas se pueden construir diferentes modelos. * I.Q.Light es una marca registrada. (Más información sobre su autor, su historia, su geometría y su comercialización en www.iqlight.com)
	Polyhedron: Este sencillo programa (no necesita instalacion), genera modelos móviles, en visión sólida o de alambre de los poliedros pitagóricos, a los que se les puede transformar mediante truncamientos, sustituir aristas o caras por vértices; obteniendo los poliedros de Arquímedes. Tiene también un juego en el que debes de conseguir poliedros a partir de otros mediante transformaciones. Inglés.		(165 Kb)
	Generador de Poliedros: Esta página web contiene una aplicación en Java con la que, a partir de los poliedros platónicos o de un polígono, y con diferentes transformaciones (truncado, extrusión, estelación) podemos conseguir vistosas figuras. Inglés. Instrucciones en Español.
CALEIDOCICLOS
	www.kaleidocycles.de/anim.shtml: Si ya conoces los caleidociclos y te gustaría ver otros diferentes sin tener que cortar y pegar papel visita esta página donde encontrarás un modelo tridimensional animado que puedes girar con el ratón para verlo por todos lados y al que puedes variar interactivamente. Muy bueno. También tiene un Applet en java que puedes descargar para trabajar sin estar conectado y plantillas para construir algunos en cartulina. Inglés. (No hace falta saber mucho para manejarlo).
OTROS
	Volumen en papel: Elaboración de figuras mediante pliegues y pegado a partir de una red de triángulos equiláteros.

domingo, 1 de febrero de 2015

RED MODULAR. TUTORIAL

TUTORIAL

TUTORIAL

4/4/11

PERSPECTIVA AXONOMÉTRICA. EJERCICIOS PARA 4º DE ESO

Usaremos como módulo el cubo, y como sistema para su representación la perspectiva axonométrica ( isométrica, dimétrica o trimétrica ). Composición modular y posterior aplicación del claroscuro.

Imprescindible la precisión y correcto uso de la escuadra y el cartabón.

Desde la siguiente imagen puedes acceder a trabajos similares de alumnos del curso pasado.

LA GEOMETRÍA DEL TOMATE EN RAMA

Al escanear este trabajo, en el que la división interna de un cuadrado nos sirve como módulo que en sucesivos giros de 90º crea una red modular, me acordé de una imagen que tenía por ahí. La imagen en cuestión es la rama que une los tomates de los llamados, y perdón por la repetición, "tomates en rama". Me pareció que ambas imágenes tenían algo en común, escaneadas, sin escalar (sin variar el tamaño de ninguna de ellas), y colocándolas una encima de otra, pude compararlas mejor. El resultado habla por sí solo, ámbas tienen en común una estructura geométrica muy similar.
Existen infinidad de ejemplos de la presencia de la geometría en la naturaleza, observa algunos ejemplos más.

9/7/09

REDES MODULARES III

Algunos trabajos más de 3º de ES0, redes creadas con módulos en los que intervienen el cuadrado y la circunferencia.

ver REDES MODULARES 1

ver REDES MODULARES 2

ver presentación de trabajos de 3º de la ESO

REDES MODULARES I

Una actividad aprentemente complicada, pero en realidad muy sencilla, es la creación de redes modulares.

Lo primero es diseñar un módulo o unidad básica, la que posteriormente repetiremos una y otra vez. El módulo se puede crear a partir de cualquier forma, aunque los polígonos regulares como el triángulo equilátero, el cuadrado y el Hexágono, son las figuras geométricas que permiten aprovechar el espacio sin dejar ningún hueco.

Después, realizamos una división interna de la forma elegida, en este caso un cuadrado.

Ya tenemos nuestro módulo, ahora tenemos que decidir de qué manera o con qué criterio vamos a repetirlo. Hay infinitas posibilidades.

Aplicando una sencilla traslación al módulo, o alternándolo con su simétrico o girándolo, tendremos soluciones como las que siguen. Son trabajos realizados por alumnos de 3º de ESO.

16/3/11

REPRESENTACIÓN DEL ESPACIO EN LA PINTURA

14/3/11

PERSPECTIVA CABALLERA: ACTIVIDADES PARA 4º DE ESO.

Desde las tres imágenes puedes acceder a la aplicación que te explicará paso a paso como realizar los ejercicios.

Estos son otros trabajos realizados por alumnos del curso anterior.

28/5/10

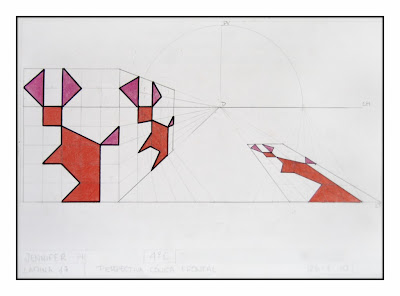
PERSPECTIVA CÓNICA FRONTRAL II: 4º DE ESO

Éste es uno de los últimos trabajos que habéis realizado en 4º C y 4ºCDiv.

Nuevamente haciendo uso de la perspectiva cónica frontal, con un planteamiento más libre que en los ejercicios anteriores y condicionado sólo por la estructura modular o cuadrícula, habéis levantado vuestras propias construcciones.

30/4/10

PERSPECTIVA CÓNICA FRONTAL: 4º DE ESO

Primer Ejercicio:

Hemos realizado el primer ejercicio sin conocer aún los fundamentos, ni todos aquellos elementos presentes en esta perspectiva ( punto principal, punto de vista, línea de tierra, plano del cuadro...):

.Un único centro de fuga y varias figuras planas (cuadrado, rectángulo...)

.Por cada uno de los vértices se trazan líneas auxiliares hasta el punto central.

.El fondo de la figura lo situamos, en este ejercicio, dónde queramos.

.Sólo hay que trazar paralelas a los lados de la figura que hemos dibujado.

Acabamos aplicando color con diferente luminosidad para potenciar el efecto tridimensional del dibujo. Y ya está. Fácil.

Segundo Ejercicio:

Conocidos los elementos gráficos de la perspectiva Cónica, habéis dibujado un plano cuadriculado situado en el plano Geometral ( el suelo), todas las líneas de la cuadrícula son paralelas al plano del cuadro ( y a LT) o bien perpendiculares ( éstas últimas fungan al punto Principal P).

Tercer Ejercicio:

Figura representada en un plano perpendicular al Plano Geometral y al Plano del cuadro:

En este trabajo podéis ver el plano representado en diferentes posiciones:

A la izquierda lo tenemos pegado al Plano del Cuadro, no se produce ninguna deformación de la figura. A continuación, el plano se ha colocado verticalmente y perpendicular al Plano del Cuadro, ahora sí se produce una alteración de la forma, al igual que en la figura de la derecha, tumbada sobre el Plano Geometral.

El siguiente vídeo explica paso a paso la contrucción de una figura en Cónica Frontal, su autor es Juan Jesús, no me preguntéis por el apellido.

ver siguiente ejercicio

6/4/10

PERSPECTIVA ISOMÉTRICA. 4º DE ESO

Siguiendo con los Sistemas de Representación habéis realizado en Perspectiva Isométrica una serie de objetos, unos inventados y otros no. El efecto tridimensional aumenta al aplicar sobre el objeto una escala tonal, los planos paralelos entre si, tendrán la misma intensidad o tonalidad.